728x90
728x90
이후에 추가로 알게된 것들을 계속 추가 할 예정이다.
인프런 강좌 내용을 참고하였습니다,
퀵 정렬 (quick sort)
퀵정렬은 분할정복 방법을 사용합니다. 분할정복방법이란 순환적(recursive)으로 문제를 푸는 하향식(top-down) 접근방법입니다.
- 분할: 배열을 pivot 을 기준으로 pivot보다 작은 값들과 pivot 보다 크거나 같은 값으로 두 부분으로 나눈다.
- 정복: 각 부분을 순환적으로 정렬한다.
- 합병: nothing to do (필요x)



슈도코드
A배열의 첫번째 원소를 p, 마지막 원소를 r로 설정한다.
마지막 수를 pivot으로 뒀을때 그 pivot이 어디에 위치해있는지 구하는 partition 함수를 이용한다.


- 검사하려는 값이 pivot보다 클때, 결국 오른쪽에 있는 원소들 값이 pivot보다 큰 값 이므로 그대로 냅두고 j 값만 하나 증가시켜준다.
- 검사하려는 값이 pivot보다 작을때, pivot 보다 작은 값들 중 마지막 값인 i 값을 하나 늘려주고 그 값을 검사하려는 값인 j와 교환시켜주고 j 값 하나를 증가시켜준다.
partition함수 최종코드

위 코드와 조금 다르지만 같은 내용이다.
- 처음 i (pivot 보다 작은 값들 중 마지막 값) 의 초기값은 p-1 이다. 아직 값이 없기 때문에
- j 는 p ~ r-1 까지 검사한다.
- i + 1 즉 pivot 위치를 반환해준다.
작동원리 사진
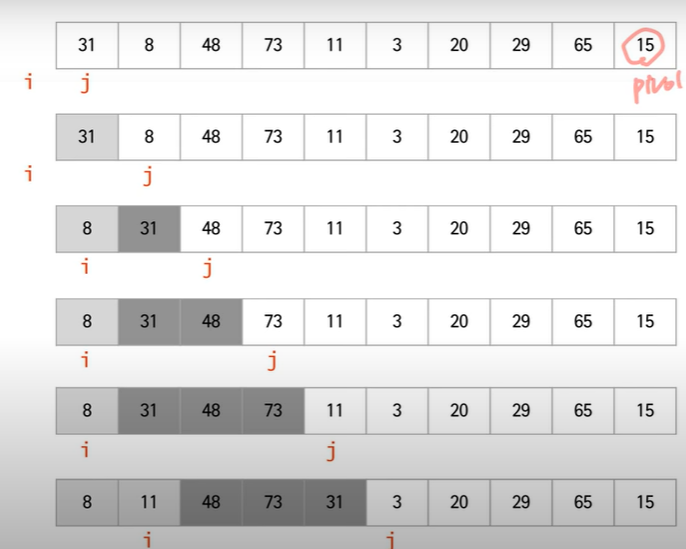
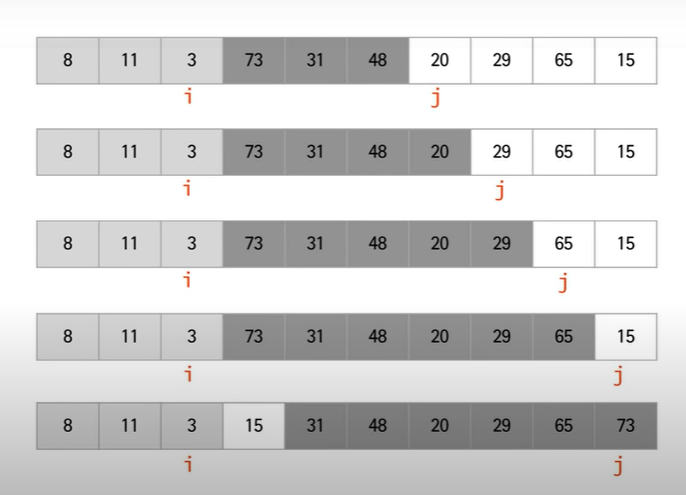
c++로 구현
#include<iostream>
using namespace std;
int a[10] = { 5,2,8,7,9,0,1,3,4,6 };
int partition(int A[], int p, int r);
void quickSort(int A[], int p, int r)
{
if (p < r){
int q = partition(A, p, r); //분할 (pivot의 위치 리턴)
quickSort(A, p, q - 1); //왼쪽 부분배열 정렬
quickSort(A, q + 1, r); //오른쪽 부분배열 정렬
}
}
int partition(int A[], int p, int r)
{
int tmp;
int x = A[r];
int i = p - 1;
for (int j = p; j <= r - 1; j++) {
if (A[j] <= x) {
i++;
tmp = A[i];
A[i] = A[j];
A[j] = tmp;
}
}
tmp = A[i + 1];
A[i + 1] = A[r];
A[r] = tmp;
return i + 1;
}
int main()
{
quickSort(a, 0, 9);
for (int i = 0; i < 10; i++) {
cout << a[i] << " ";
}
return 0;
}출력: 0 1 2 3 4 5 6 7 8 9
728x90
728x90
'개발 > 알고리즘' 카테고리의 다른 글
| [알고리즘 개념] 동적 계획법 (Dynamic Programming) -(1) (0) | 2022.07.19 |
|---|---|
| [알고리즘 개념] 삽입 정렬 (insertion sort) c++ (0) | 2022.07.19 |
| [알고리즘 개념] 버블 정렬 (bubble sort) c++ (0) | 2022.07.19 |
| [알고리즘 개념] 선택 정렬 (selection sort) c++ (0) | 2022.07.17 |